Nghiệm lại cách biểu diễn số thực trong máy tính
Sau khi học môn tin đại cương ở trường, tôi được biết về cách biểu diễn số thực theo chuẩn IEEE 754 85. Bạn nào không biết google sẽ ra. Tuy nhiên, tôi chưa được kiểm chứng ứng dụng thực tế của nó bởi chương trình học ở trường chỉ tập trung vào việc chuyển đổi cách biểu diễn các số trên giấy thôi 😂. Học cái gì cũng vậy, phải biết nó có tính thực tế mới thấy nó hay và bổ ích phải không. Cho nên hôm nay tôi quyết định làm thí nghiệm tí.
Cơ bản thì IEEE 754/85 là cách chuyển số thực dấu thành dãy các bit 0 1 để lưu trong bộ nhớ máy tính. Dãy các bit gồm 3 phần sign(1 bit), exponent, mantissa. Tùy vào độ chính xác biểu diễn mà tổng số lượng các bit và số bít của phần exponent và mantissa khác nhau. Link thêm: https://en.wikipedia.org/wiki/IEEE_754
Ở đây tôi thí nghiệm với độ chính xác là đơn, số thực sẽ được biểu diễn bằng 32 bit: 1 bit sign, 8 bit exponent, 23 bit mantissa.
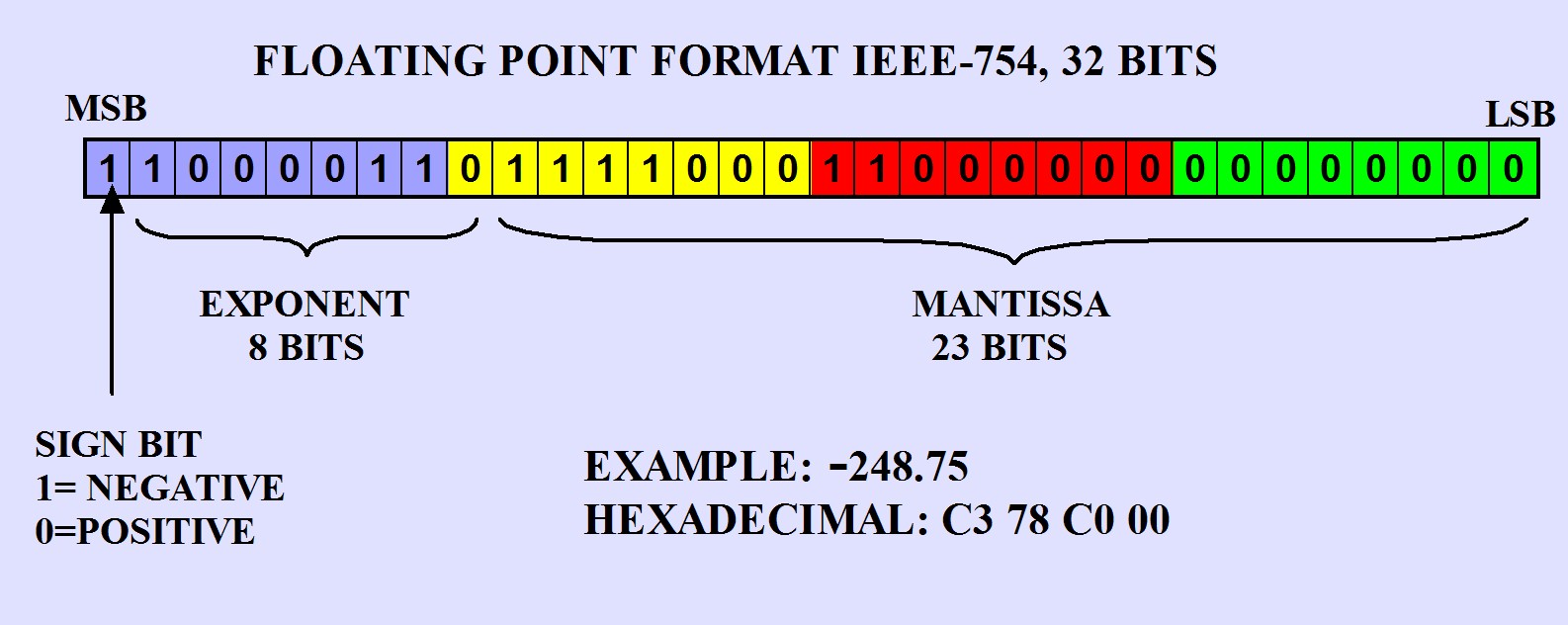
Cụ thể cách biểu diễn như thế nào ta đi vào thí nghiệm.
Tôi chọn giá trị 8.25 để cho đơn giản, sẽ giải thích sau. Dùng gdb reverse ta được.
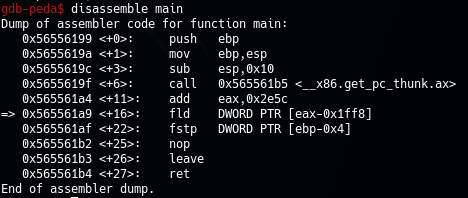
fld và fstp là 2 lệnh liên quan đến xử lí số thực trong máy tính. Tôi không đi vào phân tích 2 lệnh này bởi giờ ta chỉ cần tìm xem số 8.25 được lưu ở đâu và lưu là gì thôi cho đơn giản. Ta đã biết biến tt được lưu trong stack, nên chắc chắn [ebp-0x4] chính là vị trí của nó.
run qua lệnh fstp ta được giá trị
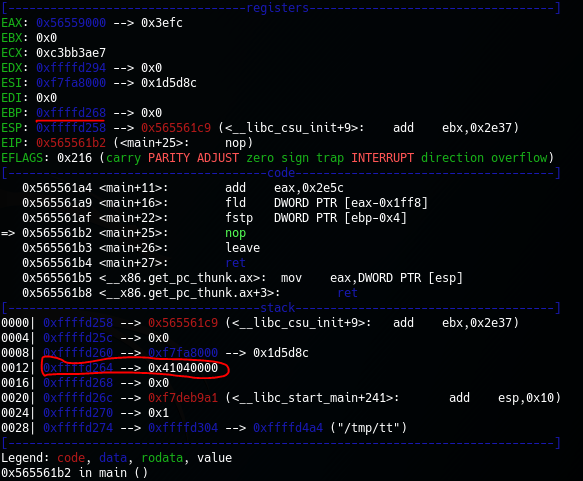
check lại
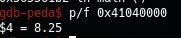
Okii giờ tiến hành phân tích
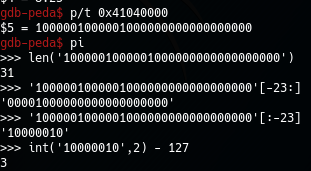
Chuyển ra nhị phân ta có 31 bit có nghĩa là bit dấu ở đầu bằng 0, đây là số dương. 8 bit tiếp theo là exponent chuyển sang hệ 10 là 130, 23 bit còn lại là mantissa ta giữ nguyên.
Để chuyển số thực về hệ 10 ta dùng công thức
với S là sign, M là số thập phân hệ 2 có phần nguyên là 1 và phần lẻ là mantissa, E là exponent trừ đi 127
Ở đây các bạn cũng nhận ra việc tôi chon 8.25 vì cơ số là 2 nên việc chuyển đổi rất dễ dàng.
Giờ ta thử với một trường hợp tổng quát hơn, -12.34 đi.
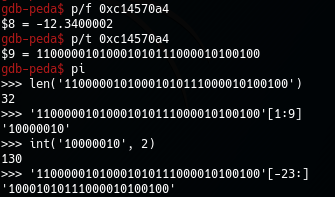
Như vậy ta cũng nhận thấy một điều là dùng cách biểu diễn này số thực sẽ có một phần sai số.